Coverage Axis: Inner Point Selection for 3D Shape Skeletonization

Abstract

In this paper, we present a simple yet effective formulation called Coverage Axis for 3D shape skeletonization. Inspired by the set cover problem, our key idea is to cover all the surface points using as few inside medial balls as possible. This formulation inherently induces a compact and expressive approximation of the Medial Axis Transform (MAT) of a given shape. Different from previous methods that rely on local approximation error, our method allows a global consideration of the overall shape structure, leading to an efficient high-level abstraction and superior robustness to noise. Another appealing aspect of our method is its capability to handle more generalized input such as point clouds and poor-quality meshes. Extensive comparisons and evaluations demonstrate the remarkable effectiveness of our method for generating compact and expressive skeletal representation to approximate the MAT.

Introduction

Pipeline of inner point selection. (a) Input 3D model. (b) Inner point candidates. (c) Dilated inner balls. (d) Selected dilated balls based on surface point coverage. (e) Selected inner balls with original radius. (f) Selected inner points.

We observe a medial sphere can be considered as an abstraction of local geometry, while the union of all the local geometries forms the entire shape. With this insight, our key idea is to formulate a Set Cover Problem, of which goal is to identify the smallest sub-collection of whose union equals the universe. Specifically, we aim to find the minimum number of dilated inner balls that cover sub-regions on the surface (i.e., sub-collection) to approximate the whole shape (i.e., universe). This formulation inherently induces a compact and expressive representation that approximates the MAT. First, the coverage constraint enforces consistency with the shape structure. Second, selecting the fewest possible candidates for shape approximation not only gives a simplified representation, but also favors the interior points that dominate larger area, which corresponds to the definition of MAT, i.e., maximally inscribed spheres.

Coverage Axis from Mesh Input

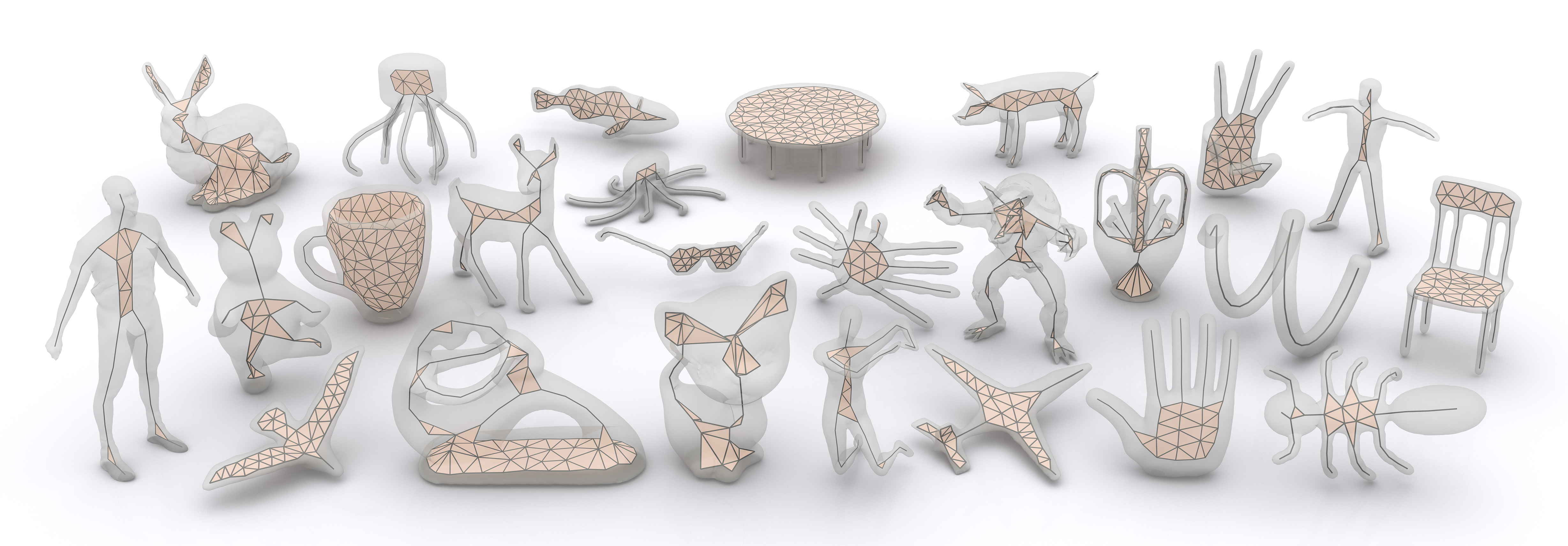
Shape approximation results of Coverage Axis. First row: the input shapes. Second row: the output skeletal representations for MAT approximation. Third row: the reconstructed shapes by the skeletal representations. Fourth row: color coding of the reconstruction error between each point in the reconstruction and the input shape, defined relative to the diagonal length of the bounding box.

Coverage Axis from Point Cloud Input

Comparison with existing shape skeletonization methods for point clouds.

More Results

Robustness to Surface Noise

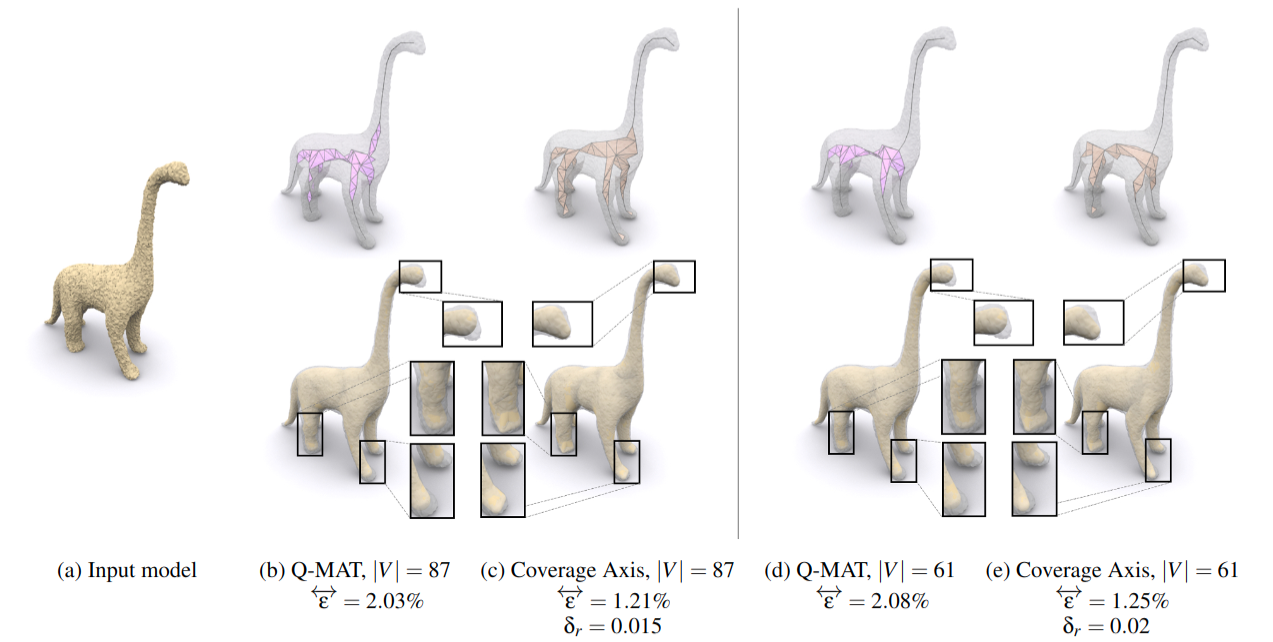
Comparison with Q-MAT on the robustness to surface noise. (a) Input model. (b)(c) and (d)(e) correspond to comparisons at different simplification levels.

Centrality and Random Initialization

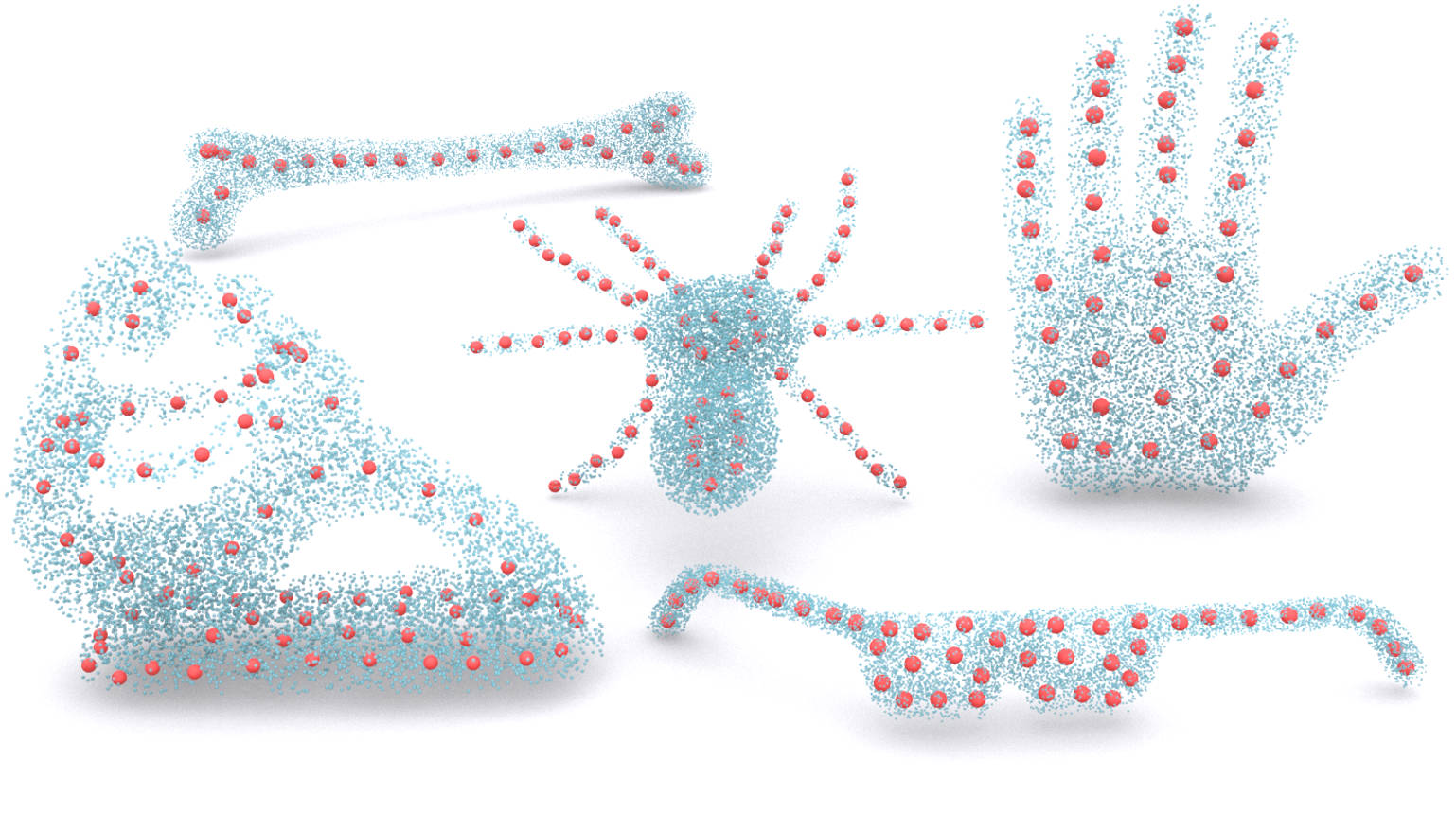
Skeletal point selection results from randomly sampled inner candidates. The blue points are candidate points generated by randomly sampling, while the orange points are selected points by our algorithm.

Divide and Conquer Strategy for Large Models

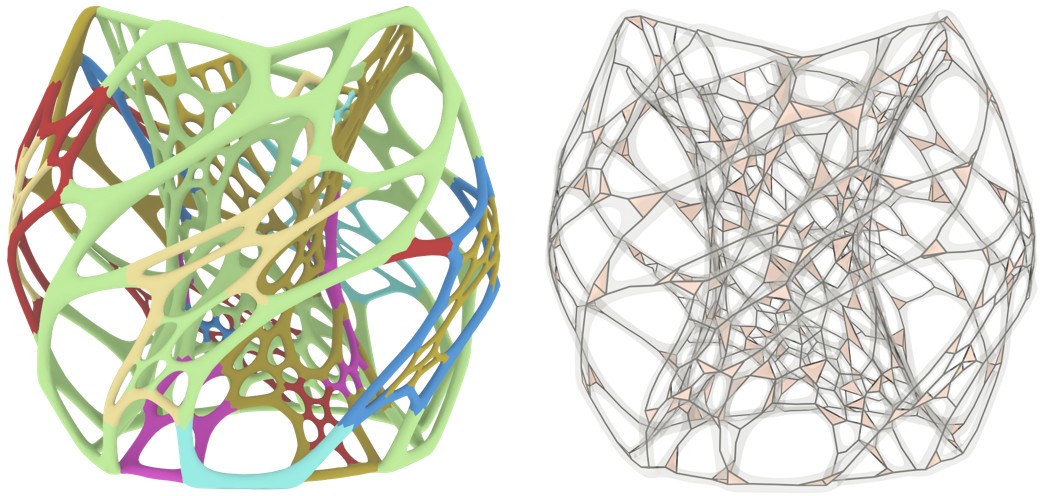
Coverage Axis with divide and conquer strategy. The model is divided into 29 parts for solving the set coverage problem separately on each part. The average running time of inner point selection of each component is 1.04 s. However, it takes more than 15 min to solve for the entire model.